本篇内容
// 计算透射度材质
compute.Dispatch(compute_transmittance, CONSTANTS.TRANSMITTANCE_WIDTH / NUM_THREADS, CONSTANTS.TRANSMITTANCE_HEIGHT / NUM_THREADS, 1);
// 计算没有经过任何散射的地面直接辐照度
compute.Dispatch(compute_direct_irradiance, CONSTANTS.IRRADIANCE_WIDTH / NUM_THREADS, CONSTANTS.IRRADIANCE_HEIGHT / NUM_THREADS, 1);
// 计算3D单次散射纹理
for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer)
{
// 计算3D texture ScatteringArray
compute.SetInt("layer", layer);
compute.Dispatch(compute_single_scattering, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
}
// 循环计算多次散射
for (int scattering_order = 2; scattering_order <= num_scattering_orders; ++scattering_order)
{
// 计算大气辐射度
for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer)
{
compute.SetInt("layer", layer);
compute.Dispatch(compute_scattering_density, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
}
// 计算来自地面的辐照度
compute.Dispatch(compute_indirect_irradiance, CONSTANTS.IRRADIANCE_WIDTH / NUM_THREADS, CONSTANTS.IRRADIANCE_HEIGHT / NUM_THREADS, 1);
// 利用上面两项计算出本阶的多次散射
for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer)
{
compute.SetInt("layer", layer);
compute.Dispatch(compute_multiple_scattering, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
}
}本篇主要讲解
计算没有经过任何散射得到的地面辐照度
单次散射的计算
Compute Direct Irradiance
这一步会用到大气渲染#1中计算得到的透射度材质,然后计算直接辐照,来自太阳的直接光经过大气传输到达地面的能量。
理论
对于间接地面辐照度,必须计算半球的积分。我们需要对半球上所有方向 ω 做积分,积分项是各方向上的乘积,即以下两项的乘积:
本来应该是经过 n 次反射后到达方向 ω 的辐照度,但这里是计算在没有散射的情况下的直接辐照度,所以应该乘以 solar_irradiance * transmittance
余弦因子,即 ωz
入口函数
#pragma kernel ComputeDirectIrradiance
[numthreads(NUM_THREADS,NUM_THREADS,1)]
void ComputeDirectIrradiance(uint3 id : SV_DispatchThreadID)
{
float2 gl_FragCoord = id.xy + float2(0.5,0.5);
deltaIrradianceWrite[id.xy] = float4(ComputeDirectIrradianceTexture(transmittanceRead, gl_FragCoord), 1);
irradianceWrite[id.xy] = float4(0,0,0,1);
if(blend[1] == 1)
irradianceWrite[id.xy] += irradianceRead[id.xy];
}各材质的意义
deltaIrradianceWrite[id.xy] = float4(ComputeDirectIrradianceTexture(transmittanceRead, gl_FragCoord), 1);
直接地面辐照度增量
irradianceWrite[id.xy] = float4(0,0,0,1);
地面辐照度累加缓存初始化
得到坐标映射
void GetRMuSFromIrradianceTextureUv(float2 uv, out Length r, out Number mu_s)
{
Number x_mu_s = GetUnitRangeFromTextureCoord(uv.x, IRRADIANCE_TEXTURE_WIDTH);
Number x_r = GetUnitRangeFromTextureCoord(uv.y, IRRADIANCE_TEXTURE_HEIGHT);
r = bottom_radius + x_r * (top_radius - bottom_radius); // Linear
mu_s = ClampCosine(2.0 * x_mu_s - 1.0);
}GetUnitRangeFromTextureCoord在第一篇中有讲到,目的是把 0.5/N ~ 1 - 0.5/N 范围的 uv 坐标映射到 0 ~ 1

然后
将 x_r 线性映射到物理参数 r:当 x_r = 0 时得到 r = bottom_radius;当 x_r = 1 时得到 r = top_radius。线性增长
将 x_μ_s 映射到[-1,1] 的区间。当 x_μ_s =0时, 2.0 × 0 - 1.0 = -1;
当 x_μ_s = 1 时, 2.0 × 1 - 1.0 = 1;
所以,x_μ_s 坐标经过映射后代表一个余弦值 mu_s 的取值范围为[一1,1]。对应θ的0~180°
计算直接辐照
IrradianceSpectrum ComputeDirectIrradiance(
TransmittanceTexture transmittance_texture,
Length r, Number mu_s)
{
Number alpha_s = sun_angular_radius / rad;
// Approximate average of the cosine factor mu_s over the visible fraction of
// the Sun disc.
Number average_cosine_factor =
mu_s < -alpha_s ? 0.0 : (mu_s > alpha_s ? mu_s :
(mu_s + alpha_s) * (mu_s + alpha_s) / (4.0 * alpha_s));
return solar_irradiance * GetTransmittanceToTopAtmosphereBoundary(transmittance_texture, r, mu_s) * average_cosine_factor;
}average_cosine_factor是一个平均余弦因子。
想想当太阳接近地平线的时候,θ是多少度?90°,那么此时mu的值,也就是cosθ = 0
太阳自身有体积,所以从他的中心到边缘会形成一个视线上的夹角,当mu(mu象征着太阳中心的位置)小于这个角的时候,说明太阳完全在地平线以下,这个时候直接返回0
反之当mu大于这个角的时候,太阳完整地在地平线以上,返回mu自身。
而当mu处于两个状态之间的时候,就采用一个近似函数(mu_s + alpha_s) * (mu_s + alpha_s) / (4.0 * alpha_s))来进行平滑过渡
最终得到的直接辐照度(这是未经过任何散射的结果)等于 solar_irradiance * GetTransmittanceToTopAtmosphereBoundary(transmittance_texture, r, mu_s) * average_cosine_factor
Compute Single Scattering
理论
第一次散射中,到达目标点p的radiance是以下五项的乘积:
太阳辐照度(solar irradiance),即大气顶上入射的太阳光强;
太阳到散射点 q 之间的大气透射率(transmittance),即大气对太阳光的衰减比例;
q 处的瑞利散射系数(Rayleigh scattering coefficient),即到达 q 的光中有多少比例会被空气分子以任意方向散射;
瑞利相位函数(Rayleigh phase function),即在所有被散射的光中,有多少比例会被定向到 p 点的视线方向;
散射点 q 到观察点 p 之间的大气透射率(transmittance),即从 q 向 p 方向出射的光到达 p 时的衰减比例。
mie散射也是同理
入口函数
#pragma kernel ComputeSingleScattering
[numthreads(NUM_THREADS,NUM_THREADS,1)]
void ComputeSingleScattering(uint3 id : SV_DispatchThreadID)
{
id.z = layer;
float3 gl_FragCoord = id + float3(0.5,0.5,0.5);
float3 deltaRayleigh, deltaMie;
ComputeSingleScatteringTexture(transmittanceRead, gl_FragCoord, deltaRayleigh, deltaMie);
deltaRayleighScatteringWrite[id] = float4(deltaRayleigh, 1);
deltaMieScatteringWrite[id] = float4(deltaMie, 1);
scatteringWrite[id] = float4(RadianceToLuminance(deltaRayleigh), RadianceToLuminance(deltaMie).r);
singleMieScatteringWrite[id] = float4(RadianceToLuminance(deltaMie), 1);
if(blend[2] == 1)
scatteringWrite[id] += scatteringRead[id];
if(blend[3] == 1)
singleMieScatteringWrite[id] += singleMieScatteringRead[id];
}每个材质的意义
deltaRayleighScatteringWrite[id] = float4(deltaRayleigh, 1);
Rayleigh 单次散射增量
deltaMieScatteringWrite[id] = float4(deltaMie, 1);
Mie 单次散射增量
scatteringWrite[id] = float4(RadianceToLuminance(deltaRayleigh), RadianceToLuminance(deltaMie).r);
Rayleigh 和 Mie 的单次散射增量转为亮度后,写入“合并的散射辐射度”纹理
singleMieScatteringWrite[id] = float4(RadianceToLuminance(deltaMie), 1);
单独把 Mie 单次散射的亮度写入一个专门的“Mie 单散射”纹理(便于后续处理)
RadianceToLuminance的作用是什么
在大气散射预计算里,“radiance” 跟 “luminance” 是两个不同层次的概念:
Radiance(辐射度)
单位通常是瓦特每平方米每球面度每纳米(W·m⁻²·sr⁻¹·nm⁻¹),描述的是光在特定波长上的能量流。
它是一个物理量,完全从能量角度出发,不考虑人眼对不同波长的不同敏感度。
Luminance(亮度)
单位是坎德拉每平方米(cd·m⁻²),是一个 光度学 量,代表“人眼看到的明亮程度”,对不同波长的光加权了人眼的亮度响应曲线(CIE 视觉匹配函数)和“光效”常数(683 lm/W)。
灯光渲染、显示设备、HDR 渲染管线、色彩管理、色调映射等都是基于光度学(人眼感知)的,而不是纯粹的物理能量。
Blend参数的意义,本质是对光谱波长做积分
其中blend的意义是:预计算的过程是按每三个波长为一组来进行计算的,如果我们预计算15个波长然后累加,那么第一波循环的blend等于0,之后都为1,意义就是叠加不同波长之间的值。
在整个预计算流程中,你会看到这样一个模式:对于一系列离散的波长 {λi} ,我们针对每一组(或者在更细化的预计算里针对每个)波长分别跑一遍完整的散射计算,然后 把这些波长的结果累加(有时还要乘以一个波长步长 Δλ)来得到最终的颜色或亮度值,这是在对光谱做积分。
int num_iterations = (NumPrecomputedWavelengths + 2) / 3;
double dlambda = (kLambdaMax - kLambdaMin) / (3.0 * num_iterations);
for (int i = 0; i < num_iterations; ++i)
{
double[] lambdas = new double[]
{
kLambdaMin + (3 * i + 0.5) * dlambda,
kLambdaMin + (3 * i + 1.5) * dlambda,
kLambdaMin + (3 * i + 2.5) * dlambda
};
// 3x3 的矩阵,预计算通常在 3 个代表性波长(例如 kLambdaR, kLambdaG, kLambdaB)下进行。当你只有 3 个波长时,需要将这 3 个波长下的辐射值转换到 sRGB 空间,这就需要一个 3×3 的转换矩阵。
double[] luminance_from_radiance = new double[]
{
Coeff(lambdas[0], 0) * dlambda, Coeff(lambdas[1], 0) * dlambda, Coeff(lambdas[2], 0) * dlambda,
Coeff(lambdas[0], 1) * dlambda, Coeff(lambdas[1], 1) * dlambda, Coeff(lambdas[2], 1) * dlambda,
Coeff(lambdas[0], 2) * dlambda, Coeff(lambdas[1], 2) * dlambda, Coeff(lambdas[2], 2) * dlambda
};
bool blend = i > 0;
Precompute(compute, buffer, lambdas, luminance_from_radiance, blend, num_scattering_orders);
}int num_iterations = (NumPrecomputedWavelengths + 2) / 3;
double dlambda = (kLambdaMax - kLambdaMin) / (3.0 * num_iterations);
for (int i = 0; i < num_iterations; ++i)
{
double[] lambdas = new double[]
{
kLambdaMin + (3 * i + 0.5) * dlambda,
kLambdaMin + (3 * i + 1.5) * dlambda,
kLambdaMin + (3 * i + 2.5) * dlambda
};
// 3x3 的矩阵,预计算通常在 3 个代表性波长(例如 kLambdaR, kLambdaG, kLambdaB)下进行。当你只有 3 个波长时,需要将这 3 个波长下的辐射值转换到 sRGB 空间,这就需要一个 3×3 的转换矩阵。
double[] luminance_from_radiance = new double[]
{
Coeff(lambdas[0], 0) * dlambda, Coeff(lambdas[1], 0) * dlambda, Coeff(lambdas[2], 0) * dlambda,
Coeff(lambdas[0], 1) * dlambda, Coeff(lambdas[1], 1) * dlambda, Coeff(lambdas[2], 1) * dlambda,
Coeff(lambdas[0], 2) * dlambda, Coeff(lambdas[1], 2) * dlambda, Coeff(lambdas[2], 2) * dlambda
};
bool blend = i > 0;
Precompute(compute, buffer, lambdas, luminance_from_radiance, blend, num_scattering_orders);
}回到正题、scattering、singleMieScattering等的含义
scattering是所有散射的汇总,而singleMieScattering是单独记录米氏散射的部分。
单次 Mie 的相位函数非常尖锐,如果把它和 Rayleigh+multi 放一起,会丢精度,也丢对 Mie 单次参数(如 g)的动态控制能力。
因此专门为单次 Mie 开了一个纹理,运行时再乘它自己的相位函数。
deltaRayleighScatteringWrite和deltaMieScatteringWrite是每轮计算的结果
以下是ComputeSingleScatteringTexture的实现:
void ComputeSingleScatteringTexture(
TransmittanceTexture transmittance_texture, float3 gl_frag_coord,
out IrradianceSpectrum rayleigh, out IrradianceSpectrum mie)
{
Length r;
Number mu;
Number mu_s;
Number nu;
bool ray_r_mu_intersects_ground;
GetRMuMuSNuFromScatteringTextureFragCoord(gl_frag_coord,
r, mu, mu_s, nu, ray_r_mu_intersects_ground);
ComputeSingleScattering(transmittance_texture,
r, mu, mu_s, nu, ray_r_mu_intersects_ground, rayleigh, mie);
}计算纹理映射(4D)
public static readonly int SCATTERING_R = 32;
public static readonly int SCATTERING_MU = 128;
public static readonly int SCATTERING_MU_S = 32;
public static readonly int SCATTERING_NU = 8;
public static readonly int SCATTERING_WIDTH = SCATTERING_NU * SCATTERING_MU_S;
public static readonly int SCATTERING_HEIGHT = SCATTERING_MU;
public static readonly int SCATTERING_DEPTH = SCATTERING_R;gl_frag_coord在这里的范围是 : x ∈ [0 + 0.5, SCATTERING_WIDTH] , y ∈ [0 + 0.5, SCATTERING_HEIGHT], z ∈ [0 + 0.5, SCATTERING_DEPTH + 0.5]。
这里需要注意的是,Compute Shader 一次只能进行一个2维运算,这里的z是第一行id.z = layer;赋值的。在Model.cs中调用Compute Shader的方式是这样的:
for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer)
{
// 计算3D texture ScatteringArray
compute.SetInt("layer", layer);
compute.Dispatch(compute_single_scattering, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
}可以看到对SCATTERING_DEPTH进行了循环,每次给layer赋值为当前3D纹理的层数
现在再来看坐标映射函数:
void GetRMuMuSNuFromScatteringTextureFragCoord(
float3 gl_frag_coord,
out Length r, out Number mu, out Number mu_s, out Number nu,
out bool ray_r_mu_intersects_ground)
{
const float4 SCATTERING_TEXTURE_SIZE = float4(
SCATTERING_TEXTURE_NU_SIZE - 1,
SCATTERING_TEXTURE_MU_S_SIZE,
SCATTERING_TEXTURE_MU_SIZE,
SCATTERING_TEXTURE_R_SIZE);
Number frag_coord_nu = floor(gl_frag_coord.x / Number(SCATTERING_TEXTURE_MU_S_SIZE)); // nu 的分辨率是 8
Number frag_coord_mu_s = mod(gl_frag_coord.x, Number(SCATTERING_TEXTURE_MU_S_SIZE)); // mu_s的分辨率是SCATTERING_TEXTURE_MU_S_SIZE
float4 uvwz = float4(frag_coord_nu, frag_coord_mu_s, gl_frag_coord.y, gl_frag_coord.z) / SCATTERING_TEXTURE_SIZE;
GetRMuMuSNuFromScatteringTextureUvwz(uvwz, r, mu, mu_s, nu, ray_r_mu_intersects_ground);
// Clamp nu to its valid range of values, given mu and mu_s.
nu = clamp(nu, mu * mu_s - sqrt((1.0 - mu * mu) * (1.0 - mu_s * mu_s)),
mu * mu_s + sqrt((1.0 - mu * mu) * (1.0 - mu_s * mu_s)));
}其中uvwz 是得到的归一化的坐标。
再看看GetRMuMuSNuFromScatteringTextureUvwz函数,能得到这四个坐标的意义:
void GetRMuMuSNuFromScatteringTextureUvwz(
float4 uvwz, out Length r, out Number mu, out Number mu_s,
out Number nu, out bool ray_r_mu_intersects_ground)
{
// Distance to top atmosphere boundary for a horizontal ray at ground level.
Length H = sqrt(top_radius * top_radius - bottom_radius * bottom_radius);
// Distance to the horizon.
Length rho = H * GetUnitRangeFromTextureCoord(uvwz.w, SCATTERING_TEXTURE_R_SIZE); // w表示0-1倍H
r = sqrt(rho * rho + bottom_radius * bottom_radius); // 长度 r 与 w有关
if (uvwz.z < 0.5) // 与地面相交
{
// Distance to the ground for the ray (r,mu), and its minimum and maximum
// values over all mu - obtained for (r,-1) 正面向下 and (r,mu_horizon) 过地平线切面 - from which
// we can recover mu:
Length d_min = r - bottom_radius; // 到地面的距离
Length d_max = rho; // 到地平线的距离
// 先1.0 - 2.0 * uvwz.z 将 0.5 - 0 映射到 0 - 1
Length d = d_min + (d_max - d_min) * GetUnitRangeFromTextureCoord(1.0 - 2.0 * uvwz.z, SCATTERING_TEXTURE_MU_SIZE / 2.0);
mu = d == 0.0 * m ? Number(-1.0) : ClampCosine(-(rho * rho + d * d) / (2.0 * r * d));
ray_r_mu_intersects_ground = true;
}
else
{
// Distance to the top atmosphere boundary for the ray (r,mu), and its
// minimum and maximum values over all mu - obtained for (r,1) and
// (r,mu_horizon) - from which we can recover mu:
Length d_min = top_radius - r;
Length d_max = rho + H;
Length d = d_min + (d_max - d_min) * GetUnitRangeFromTextureCoord(2.0 * uvwz.z - 1.0, SCATTERING_TEXTURE_MU_SIZE / 2.0);
mu = d == 0.0 * m ? Number(1.0) : ClampCosine((H * H - rho * rho - d * d) / (2.0 * r * d));
ray_r_mu_intersects_ground = false;
}
Number x_mu_s = GetUnitRangeFromTextureCoord(uvwz.y, SCATTERING_TEXTURE_MU_S_SIZE); // 映射到 0-1
Length d_min = top_radius - bottom_radius;
Length d_max = H;
Number A = -2.0 * mu_s_min * bottom_radius / (d_max - d_min);
Number a = (A - x_mu_s * A) / (1.0 + x_mu_s * A);
Length d = d_min + min(a, A) * (d_max - d_min);
mu_s = d == 0.0 * m ? Number(1.0) : ClampCosine((H * H - d * d) / (2.0 * bottom_radius * d));
nu = ClampCosine(uvwz.x * 2.0 - 1.0);
}可以看出w(gl_frag_coord.z,也就是3D材质的DEPTH)表示H的0-1倍映射,通过这个可以算出r。DEPTH对应r,高度(其实从SCATTERING_TEXTURE_R_SIZE被当做DEPTH就可以看出)
z(gl_frag_coord.y,也就是WIDTH)被分成了两段,分别计算视线与地面相交和不相交的情况。通过这个可以计算得到d,进而得到mu。也就是说WIDTH对应mu,视线方向
gl_frag_coord.x 与 nu 有关,nu是视线方向与太阳方向的余弦角,nu = ClampCosine(uvwz.x * 2.0 - 1.0);
mu_s 的计算
gl_frag_coord.x 也与 mu_s 有关,太阳方向,即太阳与法线的夹角的余弦值有关,这部分计算看上去比较复杂,我们先从它的逆映射入手:
Length d = DistanceToTopAtmosphereBoundary(bottom_radius, mu_s);
Length d_min = top_radius - bottom_radius;
Length d_max = H;
Number a = (d - d_min) / (d_max - d_min);
Number A = -2.0 * mu_s_min * bottom_radius / (d_max - d_min);
Number u_mu_s = GetTextureCoordFromUnitRange(max(1.0 - a / A, 0.0) / (1.0 + a), SCATTERING_TEXTURE_MU_S_SIZE);其中mu_s_min = Cos(MaxSunZenithAngle) ; 而 MaxSunZenithAngle = (UseHalfPrecision ? 102.0 : 120.0) / 180.0 * Mathf.PI;
这里的Cos接受弧度值。如果 UseHalfPrecision 为 false,代码中使用的是 120°:mu_s_min = cos(120°) =−0.5
如果 UseHalfPrecision 为 true,则使用 102°:mu_s_min =cos(102°)≈−0.2079。
我也没有太看懂,问了一下GPT,得到一张图:
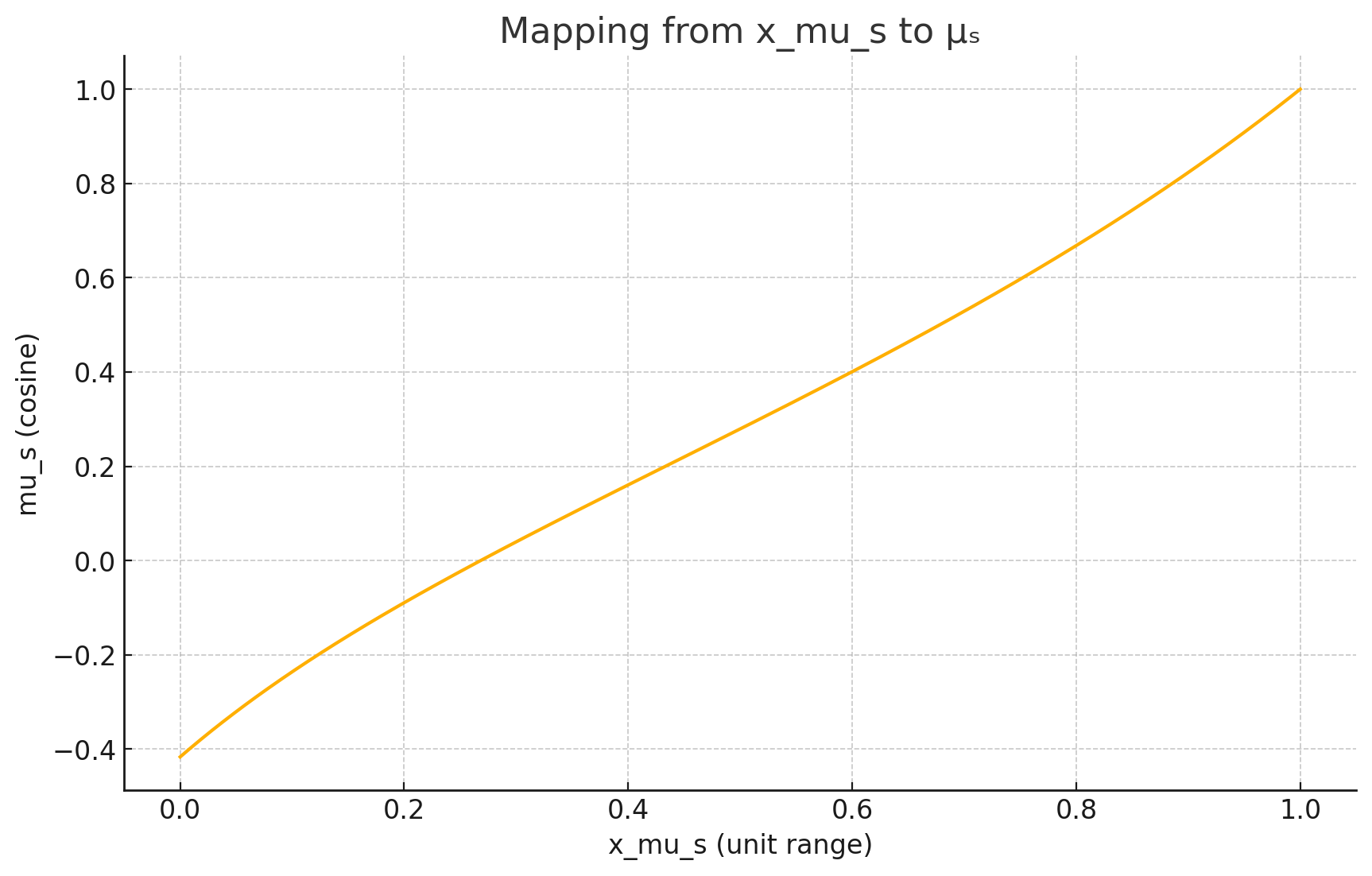
为什么要这样做
重要性采样(importance sampling):在大气散射里,靠近天顶和地平线的散射对视觉贡献更大,直接线性采样 μₛ 会导致在这些关键区域样本过疏。
非线性变换:有理函数 u′(a) 在两端具有更高的采样密度,而在中间区间保持较平缓变化,正好满足对“太阳直射”和“地平散射”区域的特殊需求。
规范nu
nu = clamp(nu, mu * mu_s - sqrt((1.0 - mu * mu) * (1.0 - mu_s * mu_s)),
mu * mu_s + sqrt((1.0 - mu * mu) * (1.0 - mu_s * mu_s)));
我之前以为,知道了mu和mu_s不就可以确定nu了吗。思考了一下发现这里不要用2D视角去想象,用3D,3D世界里你知道两个向量与法线的夹角,但他们可以旋转,所以你不知道这两个向量的夹角
计算单次散射
前面已经获得了由gl坐标映射得到的四个参数,现在利用这个参数和透射度材质来计算单次散射:
void ComputeSingleScattering(
TransmittanceTexture transmittance_texture,
Length r, Number mu, Number mu_s, Number nu,
bool ray_r_mu_intersects_ground,
out IrradianceSpectrum rayleigh, out IrradianceSpectrum mie)
{
// Number of intervals for the numerical integration.
const int SAMPLE_COUNT = 50;
// The integration step, i.e. the length of each integration interval.
Length dx = DistanceToNearestAtmosphereBoundary(r, mu, ray_r_mu_intersects_ground) / Number(SAMPLE_COUNT);
// Integration loop.
DimensionlessSpectrum rayleigh_sum = DimensionlessSpectrum(0,0,0);
DimensionlessSpectrum mie_sum = DimensionlessSpectrum(0,0,0);
for (int i = 0; i <= SAMPLE_COUNT; ++i)
{
Length d_i = Number(i) * dx;
// The Rayleigh and Mie single scattering at the current sample point.
DimensionlessSpectrum rayleigh_i;
DimensionlessSpectrum mie_i;
ComputeSingleScatteringIntegrand(transmittance_texture, r, mu, mu_s, nu, d_i, ray_r_mu_intersects_ground, rayleigh_i, mie_i);
// Sample weight (from the trapezoidal rule).
Number weight_i = (i == 0 || i == SAMPLE_COUNT) ? 0.5 : 1.0;
rayleigh_sum += rayleigh_i * weight_i;
mie_sum += mie_i * weight_i;
}
rayleigh = rayleigh_sum * dx * solar_irradiance * rayleigh_scattering;
mie = mie_sum * dx * solar_irradiance * mie_scattering;
}梯形积分原则进行积分。
到达 目标点 p 的辐照度是以下各项的乘积:
大气顶层的太阳辐照度 solar irradiance
太阳和 q 之间的透过率 transmittance (即到达大气顶层的太阳光到达 q 的比例)
q 点处的瑞利散射系数 rayleigh_scattering(即到达 q 的光线中散射出去的比例)
瑞利相函数(即散射到 目标点 p 的散射光占 q 散射光的比例),
q 到 目标点 p 之间的透射率
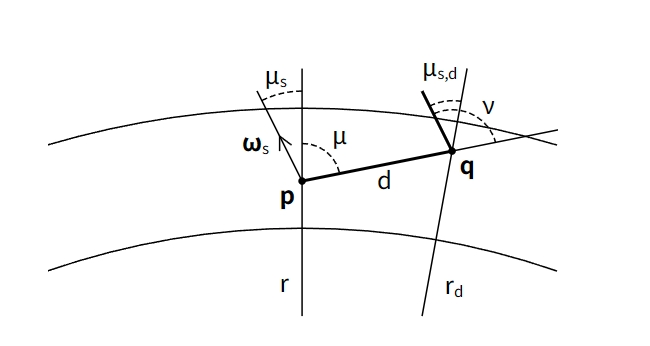
每一步积分中的几何原理
void ComputeSingleScatteringIntegrand(TransmittanceTexture transmittance_texture,
Length r, Number mu, Number mu_s, Number nu, Length d,
bool ray_r_mu_intersects_ground, out DimensionlessSpectrum rayleigh, out DimensionlessSpectrum mie)
{
Length r_d = ClampRadius(sqrt(d * d + 2.0 * r * mu * d + r * r));
Number mu_s_d = ClampCosine((r * mu_s + d * nu) / r_d);
DimensionlessSpectrum transmittance =
GetTransmittance(transmittance_texture, r, mu, d, ray_r_mu_intersects_ground) *
GetTransmittanceToSun(transmittance_texture, r_d, mu_s_d);
rayleigh = transmittance * GetProfileDensity(RayleighDensity(), r_d - bottom_radius);
mie = transmittance * GetProfileDensity(MieDensity(), r_d - bottom_radius);
}计算过程:

式子一的原理是余弦定理,式子二的原理是投影法,可以把rd乘到左边去当成投影看看。
相函数
InverseSolidAngle RayleighPhaseFunction(Number nu)
{
InverseSolidAngle k = 3.0 / (16.0 * PI * sr);
return k * (1.0 + nu * nu);
}
InverseSolidAngle MiePhaseFunction(Number g, Number nu)
{
InverseSolidAngle k = 3.0 / (8.0 * PI * sr) * (1.0 - g * g) / (2.0 + g * g);
return k * (1.0 + nu * nu) / pow(abs(1.0 + g * g - 2.0 * g * nu), 1.5);
}ν是入射方向与出射散射方向的余弦cosθ
瑞利相位函数:
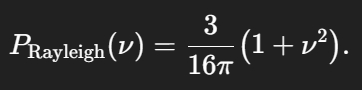
Henyey–Greenstein 近似的米氏散射相位函数:

但真正使用的相函数并非原来的正版HG函数,而是下面的:

也就是说,修改后就是在原 HG 的基础上:
多乘了一个 (1.0 + nu * nu);
再乘以一个常数 3/2 /(2 + g * g)(用来把整个函数重新归一化)。
作用是:
纯 HG 只用一个参数 g 控制前向主瓣,无法表现气溶胶的后向侧向抬升,误差可达 5–10 %。
Rayleigh 的 1+ν^2 分子项则能为后向散射提供对称抬升,但本身没有前向峰可调。
Cornette–Shanks 形式(HG × 1+ν^2)在保留 HG 前向可调主瓣的同时,引入 Rayleigh 样后向抬升,最终仅需一次代数运算、一个参数 g,加上常数 k 重新归一化,就能在 <5 % 误差内逼近真实 Mie 相位函数。
总结:这种混合模型在“性能 vs. 精度”上达到了很好的平衡,既简单高效,又比纯 HG 更贴合多峰散射特性。
LoopUp 查找材质
AbstractSpectrum GetScattering(
AbstractScatteringTexture scattering_texture,
Length r, Number mu, Number mu_s, Number nu,
bool ray_r_mu_intersects_ground)
{
float4 uvwz = GetScatteringTextureUvwzFromRMuMuSNu(r, mu, mu_s, nu, ray_r_mu_intersects_ground);
Number tex_coord_x = uvwz.x * Number(SCATTERING_TEXTURE_NU_SIZE - 1);
Number tex_x = floor(tex_coord_x);
Number lerp = tex_coord_x - tex_x;
float3 uvw0 = float3((tex_x + uvwz.y) / Number(SCATTERING_TEXTURE_NU_SIZE), uvwz.z, uvwz.w);
float3 uvw1 = float3((tex_x + 1.0 + uvwz.y) / Number(SCATTERING_TEXTURE_NU_SIZE), uvwz.z, uvwz.w);
return TEX3D(scattering_texture, uvw0).rgb * (1.0 - lerp) + TEX3D(scattering_texture, uvw1).rgb * lerp;
}每个分量都在 [0,1],并且已经过 GetTextureCoordFromUnitRange 调整到落在 texel 的中心。
真实的硬件只支持 3D 纹理,所以我们把第 1 维(ν)分成多层 slice 存放在一维纹理阵列里。查表时先:
tex_coord_x把 u_nu 拉伸到 [0,NU − 1] (u_代表是归一化坐标)tex_x—— 当前要取的 slice 下标(整数部分)lerp—— 插值因子(小数部分),用来在第tex_x层和tex_x+1层之间线性过渡,模拟 4D 的第 4 轴插值。
然后构造两次 3D 查表坐标并混合
预告
下一篇会分享MultipleScattering的学习心得。


.jpg)
